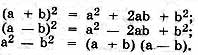НАГЛЯДНАЯ МАТЕМАТИКА
«3 в
квадрате будет 9», «3 в кубе будет 27». А вы задумывались, почему мы называем
число, умноженное само на себя, квадратом, а умноженное само на себя и еще раз
на себя — кубом? Потому что так представляли их греки. У них было, если можно
так выразиться, зрительное мышление. Недаром в греческом языке «видеть» и «знать»
были родственные слова (как в нашем — «видеть» и «ведать»). Оттого и был у
греков такой сильный страх перед бесконечностью, что ее никак нельзя вообразить
зрительно.
Нарисуйте
в вашей тетрадке число 3 в виде трех точек подряд, как на кости домино. И
подумайте: а как теперь удобнее всего нарисовать число 9? Очевидно —
пририсовать над ним еще одно такое троеточие, а потом еще одно. Получится
квадрат из 9 точек со стороной 3. Теперь возьмем три таких квадрата и положим
их друг на друга. Получится куб из 27 точек со стороной 3. Вот так видели свои
числа древние греки: как выложенные из камешков. Так что, кроме «квадратных»
чисел, у них были и «продолговатые», а кроме «кубических» — и другие «объемные».
Например, число 6 было продолговатым — как бы прямоугольником, у которого длина
3, а ширина 2. А число 30 — объемным: параллелепипедом, у которого длина 3,
ширина 2, а высота 5.
(Почему
«2 в квадрате — 4», — теперь понятно; но почему «2 — квадратный корень из
4»? Слово «корень» ввели в математику уже не греки, а арабы. Они предпочитали
представлять мир не геометрическим, как греки, а органическим; и в этом мире'из
числа 2, как растение из корня, вырастает число 4, а потом 8, а потом 16 и все
остальные степени.)
При
греческом зрительном воображении приятно было перестраивать числа из фигуры в
фигуру: например, представлять число 12 то как длинный узкий прямоугольник 6x2,
то как короткий и широкий 3x4. Поэтому греки обращали большое внимание на набор
делителей числа. Например, если число равнялось сумме собственных делителей,
оно называлось «совершенным». Греки знали четыре таких числа — 6, 28, 496 и
8128. (Если хотите, убедитесь: 6 = 1+2+3 = 1x2x3). А если из двух чисел каждое
равнялось сумме делителей другого, эти числа назывались «дружащими»: например
220 и 284. (Если хотите, проверьте: 1+2+ +4+71+142 и 1+2+4+5+10+20+11+22+44+55+110.)
Когда Пифагора спросили, что такое друг, он ответил: «Второй я» — и добавил: «Это
как 220 и 284».
Неудобства
начинались при обращении с дробями: ведь точку не раздробишь на части. Поэтому
греки предпочитали иметь дело не с дробями, а с отношениями: говорили не «одна
седьмая часть единицы», а «одна единица от семи». Отношения и пропорции они
сортировали с большой любовью. Мы говорим: «Число 20 кратно числу 5», то есть
делится на него. А грек мог вдобавок сказать: «Число 20 кратночастно числу 16»,
то есть делится на разность между ними. Вы знаете: число 4 — это среднее
арифметическое чисел 2 и 6, то есть сумма их, деленная пополам. Некоторые,
может быть, знают: число 4 — это среднее геометрическое чисел 2 и 8, то есть
квадратный корень из их произведения. А грек вдобавок знал: число 4 — это «среднее
гармоническое» чисел 3 и 6, то есть их удвоенное произведение, деленное на их
сумму.
Когда
вы начинали учить алгебру, то заучивали такие формулы, как:
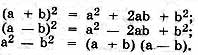Вы
помните, как они выводились? Это было довольно громоздко. А грек со своей
привычкой к наглядности доказывал их не вычислением, а чертежом: чертил отрезок
А, отрезок В, строил на них квадраты и показывал: «Вот!» Посмотрите и
убедитесь.
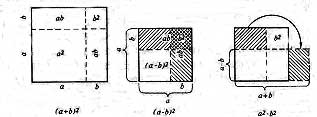Такие
геометрические доказательства выручали греков в их страхе перед бесконечностью.
Вы смогли бы, например, извлечь точный корень из числа 2? Нет, не смогли бы:
получили бы бесконечную дробь. А греческий математик поступал просто: чертил
отрезок длиной в данное число, строил вокруг квадрат, в котором он был бы
диагональю, показывал на сторону этого квадрата и говорил: «Вот!»
В
современной математике такие величины, никогда не вычисляемые до конца,
называются иррациональными. Греки называли их «невыразимые». «Невыразимым» было
отношение диагонали и стороны в квадрате — 1,41421...; «невыразимым» было и
отношение длины окружности к диаметру в круге, знаменитое число «пи» —
3,14159... («пи» — это первая буква греческого слова «периферия», окружность).
Это число изобразить было труднее, и греческие математики в своей борьбе с
бесконечностью век за веком ломали голову над «квадратурой круга»: как по
данному диаметру круга с помощью только циркуля и линейки построить квадрат,
равновеликий этому кругу?
Можно
задать вопрос: а почему, собственно, с помощью только циркуля и линейки? Не
попробовать ли изобрести новый прибор, посложнее, который позволил бы решить
эту задачу? Но грек нам гордо ответил бы: «Возиться с приборами — это дело
раба, привычного к ручному труду, а свободному человеку приличествует
полагаться лишь на силу ума».
Вот
как, оказывается, рабовладельческий образ мысли проявляется даже в такой
отвлеченной науке, как математика.
|
